2. Linear Encoding Models
- "Jehee approach"
- Fixed neural populations (fixed
- Advantage: Fit weights ( W ) with linear regression (fast! Can be done with standard fMRI analyses packages.).
- Disadvantages:
- Parameters are not interpretable
- Model mispecification?
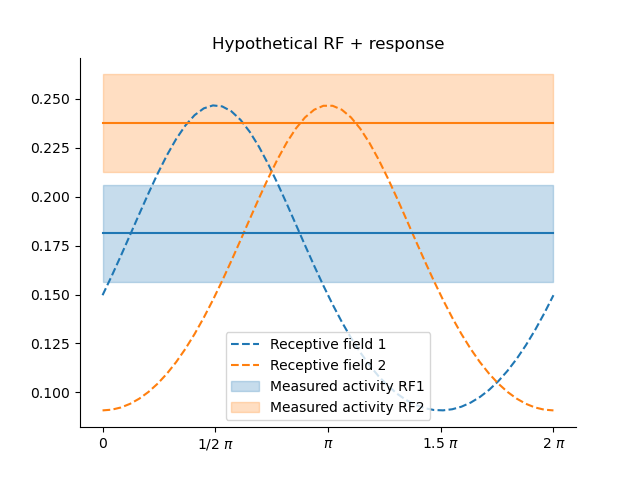
- Example: Von Mises tuning curves for orientation.
Basis Functions

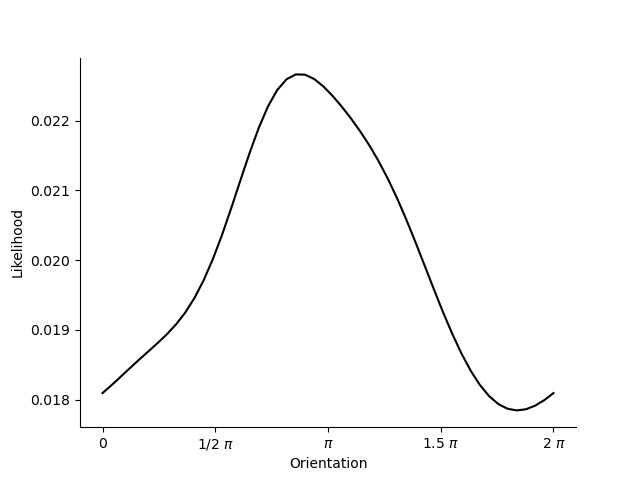
Voxel Predictions